منطق فازی (Fuzzy Logic) یکی از موضوعات جالب در دنیای هوش مصنوعی و ریاضیات است. در ادامه به توضیحی مختصر و مفید از این موضوع از جزوات و تدریس آقای دکتر فریدون شعبانی نیا میپردازم:

تعریف منطق فازی:
منطق فازی یک سیستم منطقی است که به جای استفاده از دو حالت مطلق (صفر و یک)، از درجات مختلف حقیقت استفاده میکند. این به معنای آن است که یک گزاره میتواند تا اندازهای درست یا نادرست باشد. منطق فازی اولین بار توسط دکتر لطفی زاده در دهه ۱۹۶۰ معرفی شد.

بحث کنترل فازی یا به عبارت دیگر، کاربرد منطق فازی در سیستمهای کنترل، یکی از موضوعات مهم و کاربردی در بسیاری از رشتههای علمی و مهندسی است. این علم که توسط پروفسور لطفی زاده، دانشمند ایرانی-آمریکایی، پایهگذاری شده است، در بسیاری از حوزهها مورد استفاده قرار میگیرد.
“پروفسور لطفی زاده، با نام کامل لطفی علیعسکر زاده، در سال ۱۹۲۱ در باکو، آذربایجان شوروی متولد شد و در سال ۲۰۱۷ در برکلی، کالیفرنیا درگذشت. او بنیانگذار نظریه منطق فازی است که تأثیر زیادی در علوم کامپیوتر، مهندسی برق و ریاضیات داشته است.
پروفسور زاده تحصیلات خود را در دانشگاه تهران و سپس در دانشگاه کلمبیا ادامه داد و در نهایت به عنوان استاد در دانشگاه کالیفرنیا، برکلی مشغول به کار شد. او در سال ۱۹۶۵ نظریه منطق فازی را معرفی کرد که به دلیل تواناییاش در مدیریت عدم قطعیت و پیچیدگی، در بسیاری از حوزهها از جمله کنترل فازی، هوش مصنوعی و سیستمهای خبره کاربرد دارد.”
تئوری فازی چیست؟
این تئوری به ما اجازه میدهد تا با استفاده از منطق فازی، سیستمهایی را که دارای عدم قطعیت و پیچیدگی هستند، به خوبی مدیریت کنیم. برخی از دانشمندان ریاضی و احتمالات ممکن است با این تئوری مخالف باشند، اما این مخالفتها نیاز به بحث جداگانهای دارد که فعلاً وارد آن نمیشویم.
چرا منطق فازی؟
منطق کلاسیک که با دو حالت صفر (نادرست) و یک (درست) کار میکند، برای بسیاری از مسائل پیچیده دنیای واقعی ناکافی است. منطق فازی با اجازه دادن به درجات مختلفی از حقیقت، توانایی بیشتری در مدلسازی و مدیریت عدم قطعیتها و تقریبات دارد.
کاربردهای منطق فازی:
منطق فازی در بسیاری از زمینهها کاربرد دارد، از جمله:
- کنترل فرآیندها: سیستمهای کنترلی که نیاز به مدیریت مقادیر پیوسته و غیرقطعی دارند.
- هوش مصنوعی: در سیستمهای استنتاجی و تصمیمگیری که با اطلاعات ناقص یا مبهم سروکار دارند.
- مهندسی: در طراحی سیستمهای الکترونیکی و مکانیکی که نیاز به تنظیمات دقیق و انعطافپذیر دارند.
- علوم اجتماعی و پزشکی: برای مدلسازی رفتارهای انسانی و تشخیصهای پزشکی که غالباً مبهم و چندپهلو هستند.
اجزای منطق فازی:
منطق فازی شامل سه مرحله اصلی است:
- فوزیفیکاسیون (Fuzzification): تبدیل مقادیر ورودی عددی به مجموعههای فازی.
- ارزیابی قواعد فازی (Fuzzy Rule Evaluation): اعمال قواعد فازی برای تعیین نتیجه.
- دفوزیفیکاسیون (Defuzzification): تبدیل نتایج فازی به مقادیر عددی خروجی قابل استفاده.
مزایای منطق فازی:
- انعطافپذیری بالا: توانایی مدیریت شرایط پیچیده و متغیر.
- کاربردهای گسترده: در بسیاری از صنایع و زمینههای علمی.
- مدیریت عدم قطعیت: توانایی کار با دادههای ناپایدار و غیرقطعی.
در دو دهه گذشته، تئوریهای زیادی توسعه یافتهاند و یکی از مهمترین آنها منطق فازی است. دو دلیل اصلی برای استفاده از منطق فازی وجود دارد:
- پیچیدگی سیستمها و اطلاعات فراوان: با توجه به پیچیدگی سیستمها و حجم زیاد اطلاعاتی که در اختیار ماست، که اغلب دارای عدم قطعیت هستند، نیاز به روشهای جدیدی داریم تا بتوانیم این اطلاعات را به درستی پردازش کنیم. تئوریهای قبلی برای پردازش این دادهها کافی نیستند.
- نقش انسان در سیستمهای کنترل: هرچه علوم پیشرفت میکنند، نقش انسان در سیستمهای کنترل پررنگتر میشود. بسیاری فکر میکردند که میتوان سیستمهایی طراحی کرد که بدون دخالت انسان عمل کنند، اما این ایده به طور کامل درست نیست. نقش انسان در طراحی و کنترل سیستمها همچنان بسیار مهم است.
به عنوان مثال، دو نوع هلیکوپتر وجود دارد: هلیکوپتر با خلبان و هلیکوپتر بدون خلبان. هر دوی اینها توسط انسان طراحی شدهاند و نقش انسان در کنترل آنها غیرقابل انکار است.
هدف منطق فازی این است که عملکرد مغز انسان را در سیستمها تقلید کند. این تقلید به ما کمک میکند تا سیستمهایی طراحی کنیم که بتوانند مانند مغز انسان با اطلاعات پیچیده و نامعین کار کنند.
یک سوال که معمولاً مطرح میشود این است که سیستمهای فازی Fuzzy Systems چگونه سیستمهایی هستند؟
در یک جمله میتوان گفت که سیستمهای فازی Fuzzy Systems مبتنی بر دانش یا قواعد دانش بشری Human Knowledge هستند، یعنی سیستمهایی که در طراحی آنها دانش بشری Human Knowledge نقش زیادی دارد.
علم آینده Future Science به سمتی پیش میرود که انسانها کمتر از دستهایشان استفاده کنند و بیشتر از زبان برای ارتباط با کامپیوترها و رباتها بهره ببرند. به عنوان مثال، انسان میتواند با چند کلمه به ربات فرمان دهد که غذایش را بیاورد یا لباسهایش را بشوید. این فرآیند زبانی سرعت بسیار بالاتری نسبت به فرآیند نگارش دارد و در آینده اهمیت بیشتری پیدا خواهد کرد.
امروزه نرمافزارهایی وجود دارند که میتوانند متن را از گفتار تشخیص دهند، اما این نرمافزارها هنوز مرسوم نیستند و دقت بالایی ندارند، به ویژه در زبانهای غیر از انگلیسی. بنابراین، وقتی میگوییم “Computer Work”، منظور این است که به سمتی پیش میرویم که زبان ما بتواند با سیستمهای محاسبهگر از جمله کامپیوترها ارتباط برقرار کند. منطق فازی در این راستا به ما کمک میکند.
این علم تقریباً در همه رشتههای فنی و مهندسی وجود دارد و همه از آن استفاده میکنند. یکی از رشتههایی که بیشتر از منطق فازی استفاده میکند، مهندسی کنترل است. همچنین، در علوم پزشکی نیز منطق فازی کاربرد زیادی پیدا کرده است.
پرسش اول این است که فازی چیست؟ وقتی سیستم دادهها یا اطلاعات ما دارای نامعینی باشد، آن دادهها را فازی مینامیم. لغت فازی در لغتنامه آکسفورد به معانی مختلفی آمده است، از جمله “در هم”، “کرکی”، “غیر دقیق” و “ابهام”. این لغتها نشاندهنده عدم شفافیت Lack of Transparency و نامعینی در دادهها هستند.
در ایران نیز از همان لغت فازی استفاده میشود، زیرا معادل دقیقی برای آن وجود ندارد. به روایت آقای دکتر شعبانینیا از لغت “عدم شفافیت” Lack of Transparency استفاده میکنند، اما این لغت در سیستمها معنی دقیقی ندارد. بنابراین، لغت فازی به خوبی گویای این مفهوم است.
یک مثال واضح و روشن که همه ما به طور روزمره با آن سر و کار داریم، رانندگی است. فرض کنید دو راننده داریم: یکی که ذهنش بسیار دقیق است و دیگری که انعطافپذیری بیشتری دارد. به طور مثال، افرادی که در پادگانها بزرگ میشوند، معمولاً بسیار منظم و دقیق هستند، در حالی که افرادی که خارج از پادگانها زندگی میکنند، ممکن است این دقت را نداشته باشند.
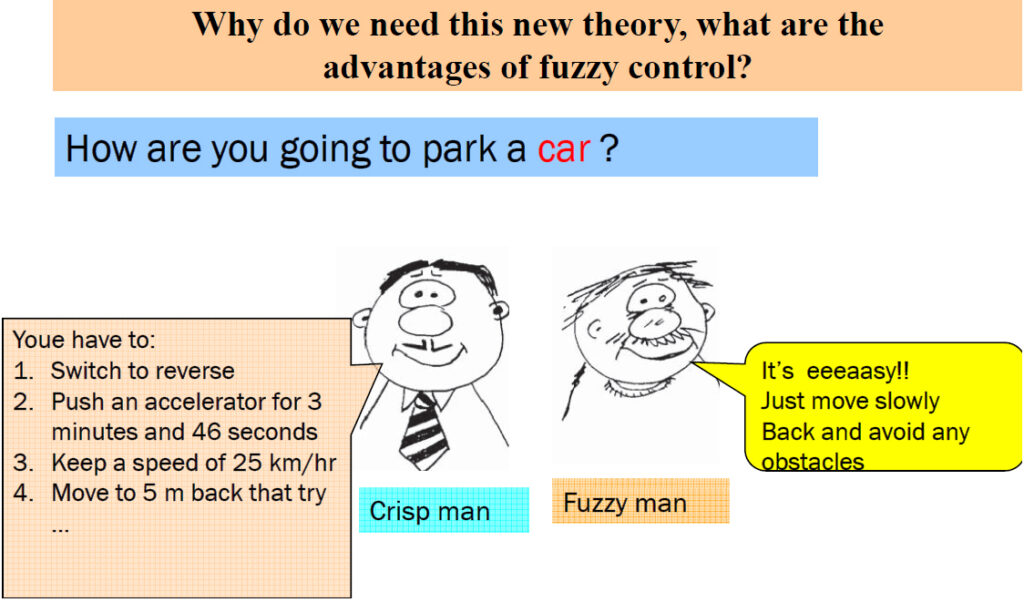
میخواهیم بررسی کنیم که یک فرد دقیق چگونه رانندگی میکند و خروجی کدام بهتر است. نمیخواهم بحث فلسفی داشته باشم، اما گاهی نظم و انضباط خوب است و گاهی نیاز به انعطافپذیری (Flexibility) داریم.
فرض کنید دو راننده داریم: یکی که به صورت کریسپ (Crisp) و دقیق رانندگی میکند و دیگری که به صورت فازی (Fuzzy) و انعطافپذیر رانندگی میکند. فردی که کریسپ است، ممکن است بگوید: “سوئیچ را به حالت دنده عقب ببر، در زمان دو دقیقه و ۴۶ ثانیه فشار بده روی پدال گاز (Accelerator)، سرعت را به ۲۵ کیلومتر در ساعت برسان و سه متر عقب برو.” حالا اگر نشد، دوباره همین روش را تکرار کند. اما چند درصد رانندهها میتوانند این دستورالعمل دقیق را دنبال کنند؟
ما نمیخواهیم همه امور زندگیمان را بر اساس دقت صددرصد پیاده کنیم. دقت و سرعت خوب هستند، اما گاهی نیاز به تفکر فازی (Fuzzy Thinking) داریم. رانندگی چیزی نیست که شما بخواهید به طور صددرصد دقت به خرج دهید. کنترلرهایی که برای خودروهای بدون سرنشین (Autonomous Vehicles) ساخته میشوند، دقیقاً از کنترل فازی (Fuzzy Control) استفاده میکنند. آینده این خودروها از همین تئوریها استفاده میکند و منطق فازی یکی از آنهاست.
بنابراین، فرد کریسپ ممکن است پارکینگ را به دقت انجام دهد، اما چند درصد جامعه میتوانند از یک فرمول خاص برای پارک کردن خودرو استفاده کنند؟ شما به عنوان یک شاگرد رانندگی، اگر مربی شما با این دقت و سختگیری برخورد کند، احتمالاً جلسه دوم دیگر نمیروید.
این نکات اساسی هستند که نشان میدهند ما نمیخواهیم منطق فازی را در همه جا پیاده کنیم، اما در بسیاری از موارد، این منطق میتواند بسیار مفید باشد.
فازی اینجا به درد ما میخورد که کاربرد برای ما ندارد، اما فرد دوم، قیافهاش را نگاه کنید. وقتی قیافهاش اینطوری داده شده، این معنیش این نیست که ژولیده است. میخواهد بگوید که این فرد فازی تینکینگ (Fuzzy Thinking) دارد. در حقیقت، یک اختلاف بین این فرد و آن فرد هست. اما این فرد برمیگردد و خیلی ساده به شما میگوید: “ایزی، خیلی ساده است. شما مراقب باش به کسی نزنی.” ذهنش تجربهای دارد که یاد گرفته چکار بکند و نیازی به فرمول ندارد. به هیچ وجه، با دو سه مرتبه عقب جلو راحت پارک میکند.
حالا از شما بپرسم، خب شما چطور پارک میکنید؟ شاید نتوانید به من بگویید طبق این کریسپ (Crisp) که دقیقاً چه کار میکنید. فازی تینکینگ (Fuzzy Thinking) همین است. این انسان به راحتی خودش را ادپت (Adapt) میکند و این همان چیزی است که میخواهم بگویم.
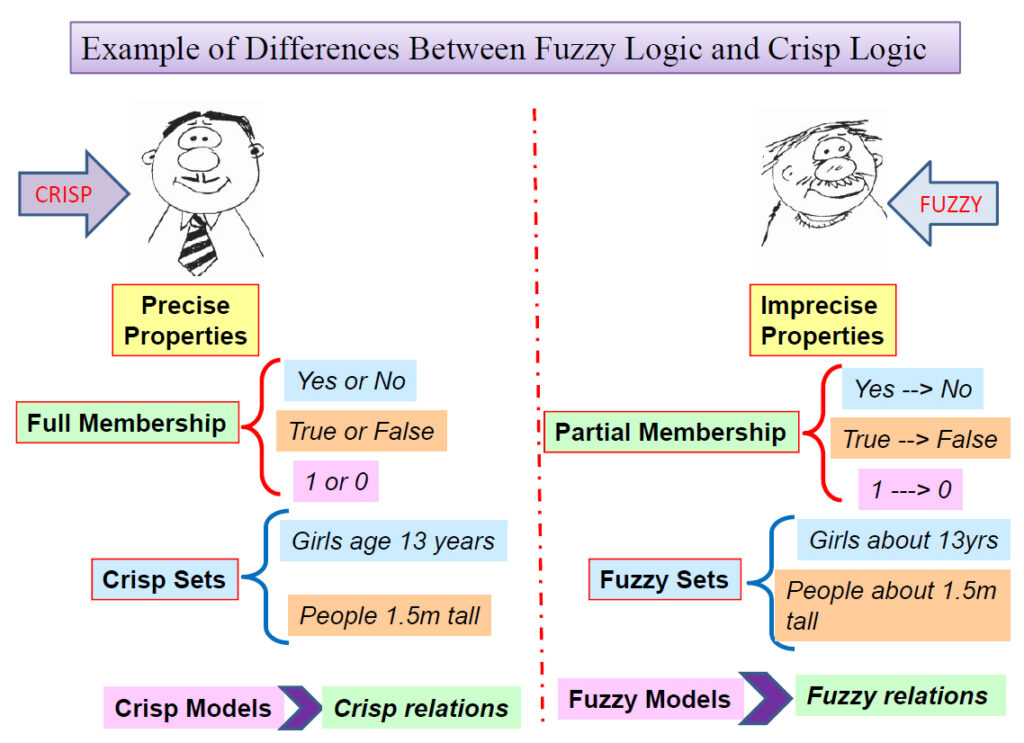
آبجکت (Object) شیء میتواند یک تابعی بگیرد، یک تابع عضویتی به آن تعلق بگیرد، یا صفر است یا یک. مثلاً از شما خواسته میشود یک سری سیب دارید و یک سری پرتقال. اینها را با استفاده از مجموعهها میگوید سیبها را من قرار میدهم یک تابع عضویت یک و پرتقالها را قرار میدهم تا عضویت صفر. این بحث فول ممبرشیپ (Full Membership) برای بخشی از اشیا قابل پیاده کردن است. از جمله سوالی که مطرح میشود اینکه خوب، شما اگر بخواهید پرتقالها با سایزهای مختلف را با استفاده از مجموعهها تقسیم بکنید، جوابی برایش ندارید. منطق این مسئله را برایتان حل میکند. در نتیجه ما بحثی داریم به نام فبرشیپ (Fuzzy Membership)، بحثی داریم به نام پارشال ممبرشیپ (Partial Membership)، عضویت جزئی. بحثی خواهیم داشت به نام کریسپ (Crisp) مجموعههای صفر و یک. بحث خواهیم داشت به نام فازی ست (Fuzzy Set) مجموعههای فازی. به نام روابط دقیق، روابط دودویی و بحث دیگری خواهیم داشت تحت عنوان فاز ریلیشن (Fuzzy Relation) روابط فازی.
آقای لطفی زاده وقتی سال ۱۹۶۵ آمد مجموعههای فازی را تعریف کرد، اشکالات زیادی آن مجموعههای فازی داشت. قضیههایی را که ایشان آنجا آورده بود با یک سری اشکالاتی همراه بود. حدود ده سال با مشکلات زیادی ایشان روبرو شد. درگیریهای زیادی پیدا کرد. ولی بعد از ۱۰ سال آمده بود آن ضعفهایی که وجود داشت در آن مجموعههای فازی برطرف کرد. حالا میبینیم در سالهای ۱۹۸۱ به بعد منطق فازی تقریباً جهانگیر میشود.
مثال، در این مثال به دو مفهوم دقت (Precision) و اهمیت (Significance) اشاره داریم و توضیح =میدهیم که چگونه این دو مفهوم میتوانند در موقعیتهای مختلف کاربرد داشته باشند.
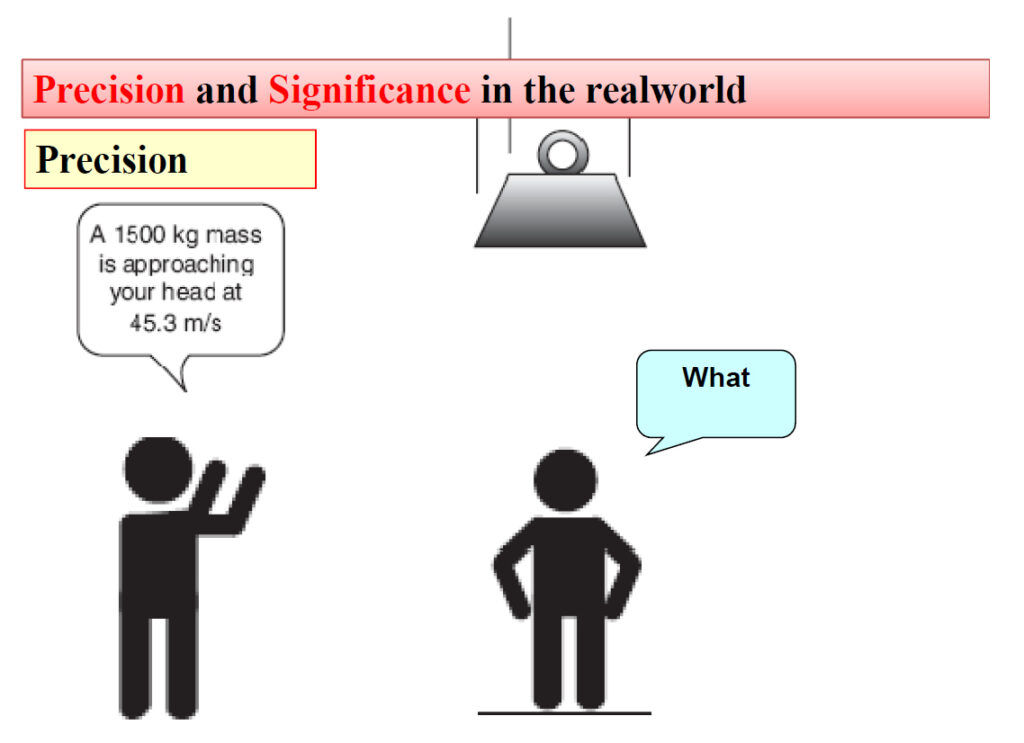
برای روشنتر شدن موضوع، مثالی از یک فرد که در زیر یک جرثقیل ایستاده و بار به سمت او حرکت میکند، ارائه میدهم. فرض کنید شما در یک جایی ایستادهاید و یک ساختمان چند طبقه در حال ساخته شدن است. توسط این جرثقیلها، بار از پایین به طبقات بالا انتقال داده میشود، مثلاً سیمان، آجر و غیره. حالا یک فردی هم پایین ایستاده است و متوجه نیست که بار به سمت او حرکت میکند. شما این مسئله را میبینید و میخواهید او را از خطر مرگ نجات دهید.
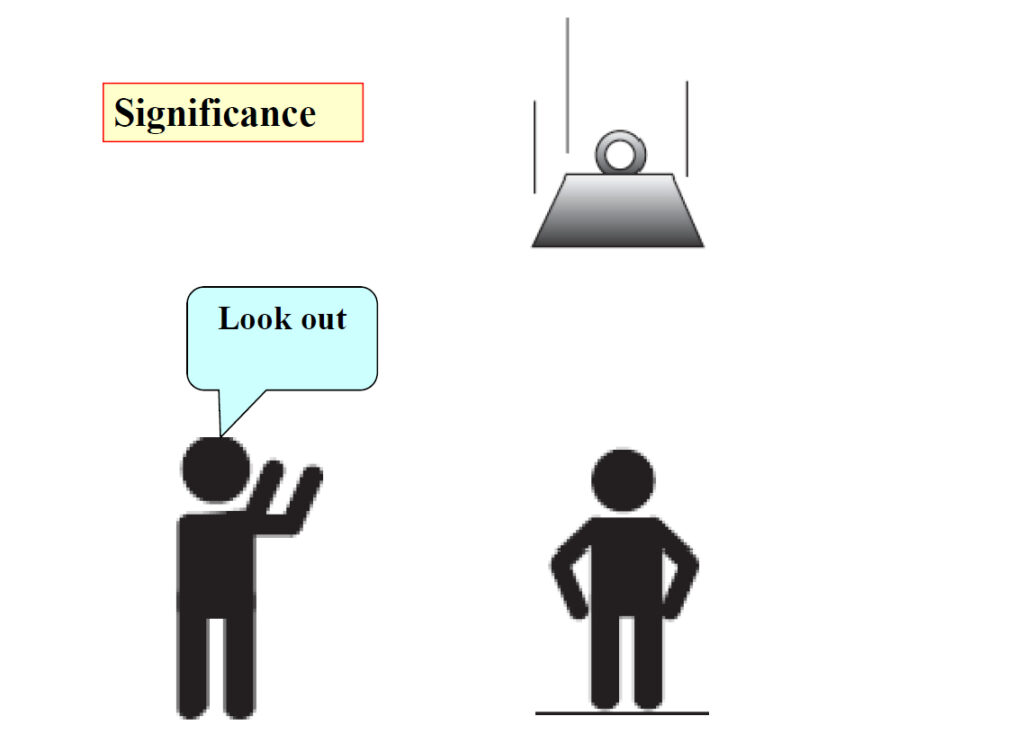
اگر بخواهید با دقت کامل هشدار دهید، ممکن است بگویید: “یک وزنه ۱۵۰۰ کیلویی با سرعت ۴۵.۳ متر در ثانیه به سمت تو میآید.” این جملهبندی دقیق است و اطلاعات کاملی ارائه میدهد، اما تا زمانی که این جمله به گوش فرد برسد و او مفهوم آن را بفهمد، ممکن است اتفاق افتاده باشد. این میشود Precision .
اما شما میتوانید با یک جمله خیلی ساده بگویید: “لوک اوت!” (Look out!). این لغت در این صحنه مفهوم بالایی دارد و هم برای شما و هم برای آن فرد قابل فهم است. وزنه سنگین به سمت او میرود و با این هشدار ساده، او میتواند از مهلکه رهایی پیدا کند.
بنابراین، وقتی از این لغات استفاده میکنیم، باید بدانیم در جاهای مختلف چگونه از آنها استفاده کنیم. این فهم خودمان را باید به سیستمها منتقل کنیم. سیستمها دارای نامعینی هستند و ما نمیتوانیم به اجبار یک سیستم را نامعین کنیم. طبیعت این سیستمها دارای نامعینی است. به همین دلیل، باید منطق فازی و تئوری فازی را در جاهایی استفاده کنیم که کاربردش به وضوح دیده میشود.
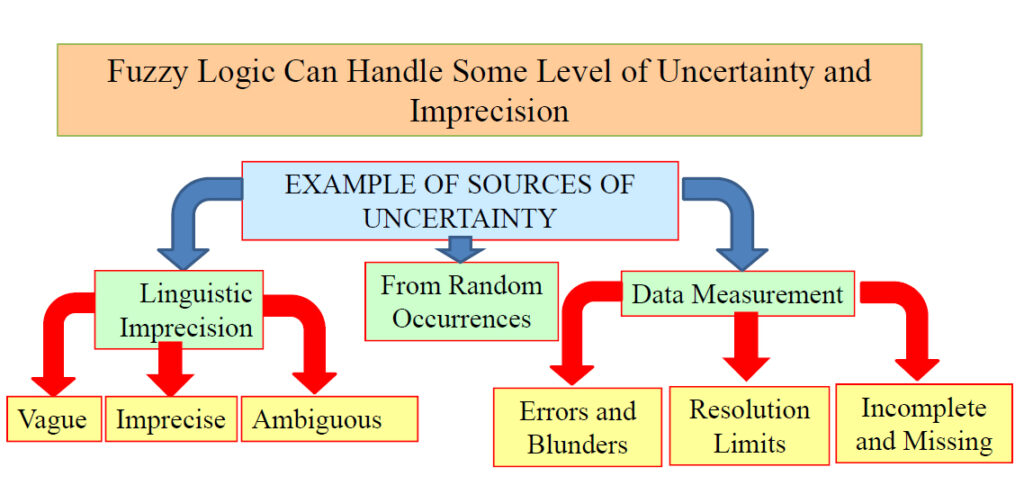
نکات کلیدی عبارتند از:
- منطق فازی: به دلیل تواناییاش در مدیریت عدم قطعیت و ابهام، در بسیاری از زمینهها از جمله هوش مصنوعی، کنترل سیستمها و تصمیمگیری استفاده میشود.
- دادههای نامعین: در مهندسی شیمی، دادههای اندازهگیری شده ممکن است به دلیل تغییرات محیطی و خطاهای اندازهگیری نامعین باشند.
- منابع نامعینی: این منابع شامل خطاهای اندازهگیری، رزولوشن دستگاهها و عدم توانایی در اندازهگیری همزمان متغیرهای مختلف است.

